W01 課程介紹
2024-09-11-Wednesday 14:10-17:00 林師模教授 shihmolin@gmail.com (助教Sopia張桂鳳)
| GoogleDoc-Note | Presentation | Paper/Report |
Review of basic statistics concept | A_Review_of_BasicStatistical_Concepts | 統計テスト | Prof.'s: Basic Probability Concepts |
預習: 參考 自習Econometrix and 變量分析 Multivariate Analysis | 五分鐘R語言系列第一集: 安裝下載及簡 | 閱讀筆記 Hackmd |
網頁: 統計學-自習 | Regression Analysis 回歸分析 | Research Methods預習 |
課本: 全文 Principles of Econometrics, 5th Edition | 參考資料查表(Statistical Tables和Formula Sheets) 等等 | EViews_prgprogram files |
By chapter:
Chp00|
Chp01|
Chp02|
Chp03|
Chp04|
Chp05|
Chp06|
Chp07|
Chp08|
Chp09|
Chp10|
Chp11|
Chp12|
Chp13|
Chp14|
Chp15|
Chp16|
Appendix|
GDoc_chp04 |
GDoc_chp05 |
查表: F-critical_value |
軟體: EViews | EViews Alternatives for Linux | 🎯 李宗璋老師Youtube的EViews教學 |
練習: GoogleSheet-Exc#1 | Exc#2 |
作業: Asig#1 | W08Asig#2 | W11Asig#3 | W14Asig#4 | W16 12/25 Asig#5-Final Report |
Asig#5-期末的 QM_Final Asig#5_作業草稿 | 老師建議 與Asign#5相關的論文參考html 詳讀 | Asig#5 報告完稿 | 計算用GoogleSheets | AugustineAsig#5作業供參考 |
2025/01/06 Asig#5 交出的作業pdf |
Romi llham 提供的 Quantitative Methods I 預習參考。 | Reyner 提供 資格考參考 |
EViews 與 Weka 的比較
EViews(Econometric
Views)是一款由QMS公司開發的計量經濟學和統計分析軟體,主要用於時間序列分析、橫截面數據分析和面板數據分析。其主要功能包括:
• 資料管理:可以方便地輸入、擴展和修改時間序列數據或橫截面數據。
•
統計分析:提供多種統計分析方法,如複迴歸分析、敘述統計、假設檢定等。
• 預測分析:能夠進行時間序列的預測和模擬。
•
圖形化界面:直觀的圖形用戶界面,支持Excel、SPSS、SAS等文件格式的匯入和匯出
1
EViews 統計分析軟體應用簡介
2
Eviews 操作簡介
3 Eviews簡介
李宗璋老師講Eviews 1暨南大學統計學碩士,華南理工大學管理學博士,現任教於華南農業大學經濟管理學院。
Weka
Weka(Waikato Environment for Knowledge Analysis)是由新西蘭懷卡托大學開發的開源資料探勘軟體,主要用於機器學習和數據挖掘。其主要功能包括:
• 資料處理:支持多種數據文件格式,如CSV、ARFF等,並提供數據預處理工具。
• 特徵選擇:提供多種特徵選擇方法,幫助選擇最具代表性的特徵。
• 分類和回歸:內建多種分類和回歸算法,如決策樹、隨機森林、支持向量機等。
• 聚類和關聯規則:支持分群分析和關聯規則探勘。
• 可視化:提供數據和模型的可視化工具,便於分析結果的展示
4 Weka簡介與實作:
5 Weka机器学习使用介绍(数据+算法+实战)
6 数据处理、特征选择、分类、回归、可视化 。
異同比較
• EViews:主要用於經濟學和金融領域的計量經濟分析。功能側重於時間序列分析和經濟模型的構建與預測。
• Weka:廣用於資料探勘和機器學習,如金融、醫療、營銷等。提供豐富的算法和數據處理工具。
Introduction
Review of basic statistics concepts (1)
W02 Review of basic statistics concept (2), ANOVA
The simple linear regression model (1)
2024-09-18-Wednesday 14:10-17:00 林師模教授 (助教Sophia張桂鳳)
W03 單因子變異數分析 One-way ANOVA
2024-09-25-Wednesday 14:10-17:00 林師模教授
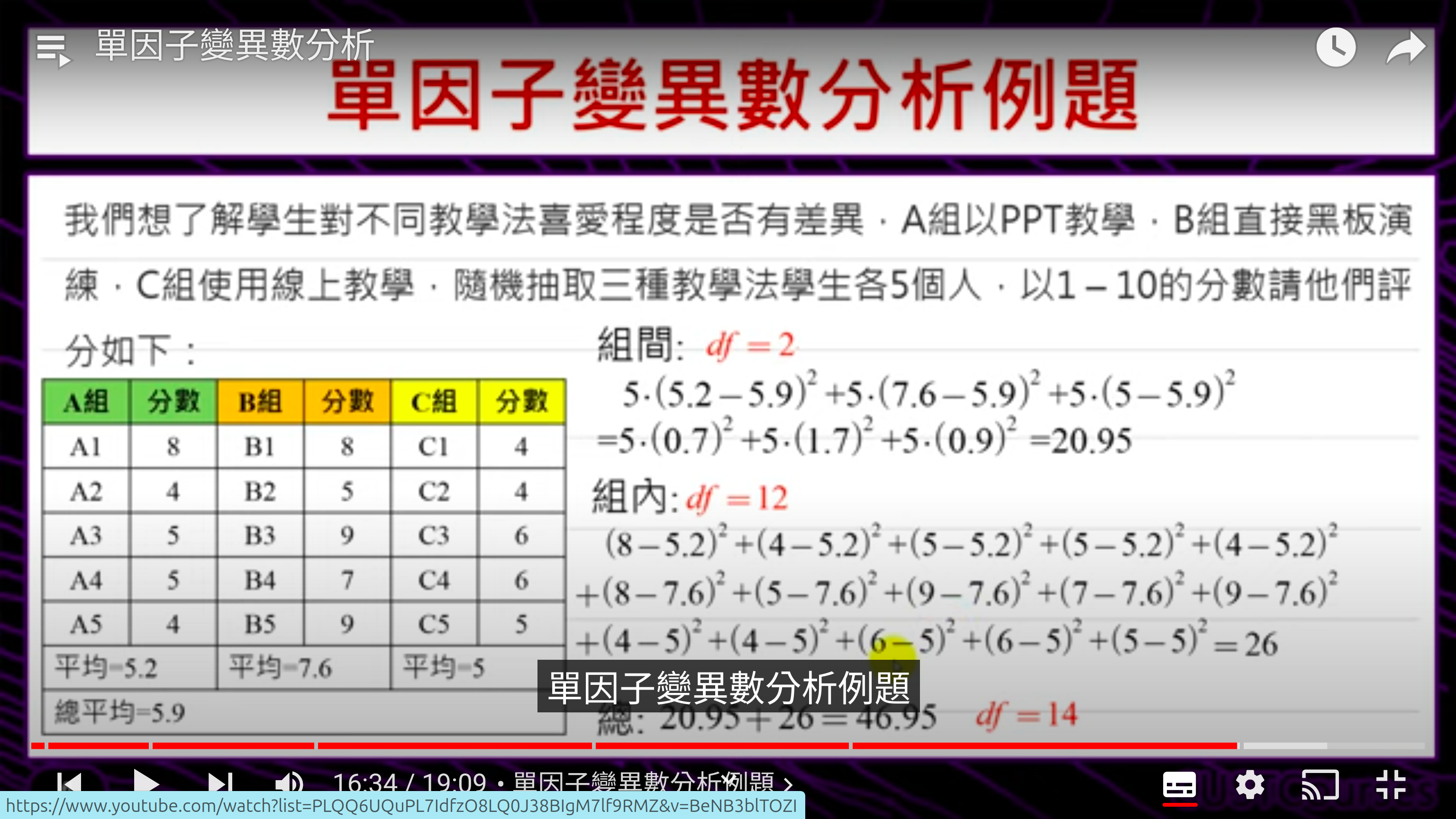
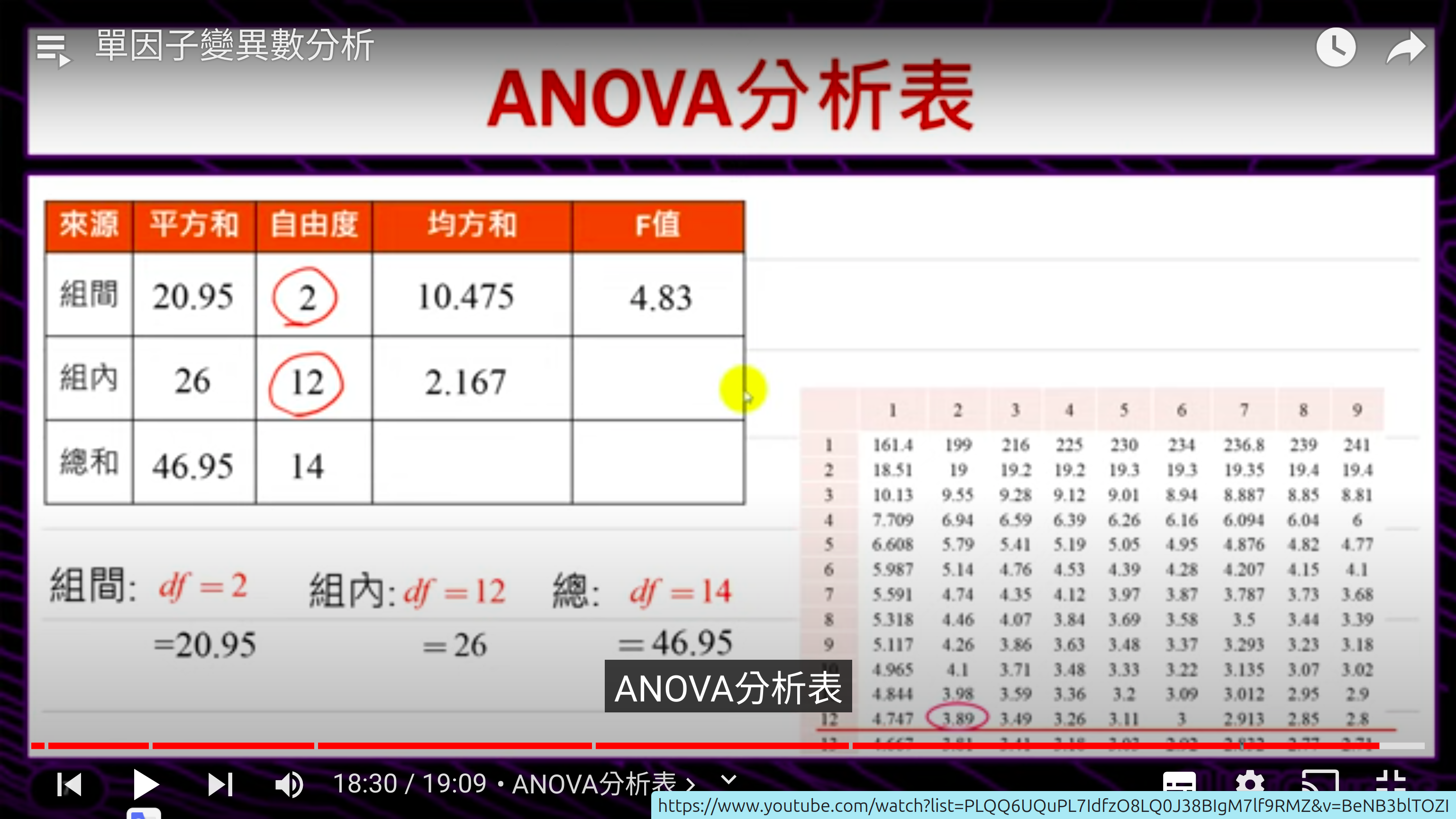
ANOVA 李柏堅單因子變異數分析One-way ANOVA
 |
 |
1.Hypothesis Test
2.Analysis of Variance
1.Hypothesis Test: (how much doubt does this cast on Justin's hypothesis?)
1) Question? 比如你已有100學生 兩種成績 也知學生來自北中南區,想知:
wether region will effect the score?
2) Null Hypothesis (μN = μC = μS) = H0
Alternative will be: any pair of those 3 are not equal
3) Test statistic (可以自己想辦法比較, 參考別人經驗, 搬用書本案例)
testing (do probability testing ) need to know probability distribution
要做statistic先要知道probability distribution
4) significant level (α) 1% 5% 10% usually 5%
if hypothesis is true but eventually we reject the hypothesis
"the chance of making error is 5%"
you can check the table to see the critical value (critical point臨界點 值 )
acceptance area 95% --critical value-- rejection area 5%
5) Ho = (μN = μC = μS) make decision of reject or not
2.Analysis of Variance
Definition of ANOVA: Analysis of variance (ANOVA) is a statistical test used to assess the difference between the means of more than two groups.
"analysis of variance but the purpose is compare the mean."
compare the any observe sample, how far is it from the total mean.
- cancel out
- sum squat total SST
- SSE error sum square
- SSB between group
- 如果三個group大不同 SSB 應該會大 (SST=SSE+SSB) 因各group的mean離total mean遠
知道這個道理後,思考怎樣 設計(發展)出一個 measure ?
W04 Hypothesis testing (1)
2024-10-02-Wednesday 14:10-17:00 林師模教授
 模型的五個基本假設(SR1–SR5)如下:
模型的五個基本假設(SR1–SR5)如下:1. SR1: 線性模型假設 - 這假設模型是線性的,即因變數 (Y) 和自變數 (X) 之間的關係可以表示為 (Y = \beta_0 + \beta_1 X + u),其中 (u) 是誤差項。
2. SR2: 隨機抽樣假設 - 假設樣本數據是從總體中隨機抽取的,這確保了樣本具有代表性。
3. SR3: 誤差項的期望值為零 - 假設誤差項 (u) 的期望值為零,即 (E(u) = 0)。這意味著在所有觀測值中,誤差項的平均值為零,不會系統性地偏向某一方向。
4. SR4: 同方差性假設 - 假設誤差項的方差是恆定的,即 (Var(u) = \sigma^2)。這意味著所有觀測值的誤差項具有相同的變異程度。
5. SR5: 誤差項的獨立性假設 - 假設誤差項之間是相互獨立的,即 (Cov(u_i, u_j) = 0) 當 (i \neq j)。這意味著一個觀測值的誤差項不會影響另一個觀測值的誤差項。
這些假設是簡單回歸模型的基礎,確保了模型估計的有效性和可靠性。如果這些假設被違反,可能需要使用更複雜的模型或方法來進行修正。
另有一個 SR6 是一個可選的假設,通常被稱為正態性假設。這假設誤差項 (u) 服從正態分佈,即 (u \sim N(0, \sigma^2))。這意味著誤差項不僅期望值為零且具有恆定方差,還應該呈現鐘形的正態分佈。這個假設的主要作用是:
1. 簡化推論:正態性假設使得許多統計推論方法(如t檢驗和F檢驗)更加簡單和有效。
2. 提高估計效率:在正態性假設下,最小二乘估計量(OLS)是最有效的線性無偏估計量(BLUE)。
然而,正態性假設並不是必需的,許多回歸分析方法在誤差項不正態分佈的情況下仍然有效。

W05 Simple Linear Regression Model
2024-10-09-Wednesday 14:10-17:00 林師模教授
Ch-02 Simple Linear Regression Model
- Mastering Econometrics with Joshua Angrist
- 有例題可作 簡單線性迴歸分析
- University of West Georgia Linear_regression_Notes
W06 Goodness-of-fit and modeling issues (1)
2024-10-16-Wednesday 14:10-17:00 林師模教授
Ch-03
W07 Chapter3: Interval Estimation and Hypothesis Testing
2024-10-23-Wednesday 14:10-17:00 林師模教授
Ch-02
Ch-03
當你在 EViews
中進行收入(INCOME)與食品支出(FOOD_EXP)的普通最小二乘法(OLS)回歸分析時,得到的統計結果可以幫助你理解兩者之間的關係。以下是每個統計量的解釋:
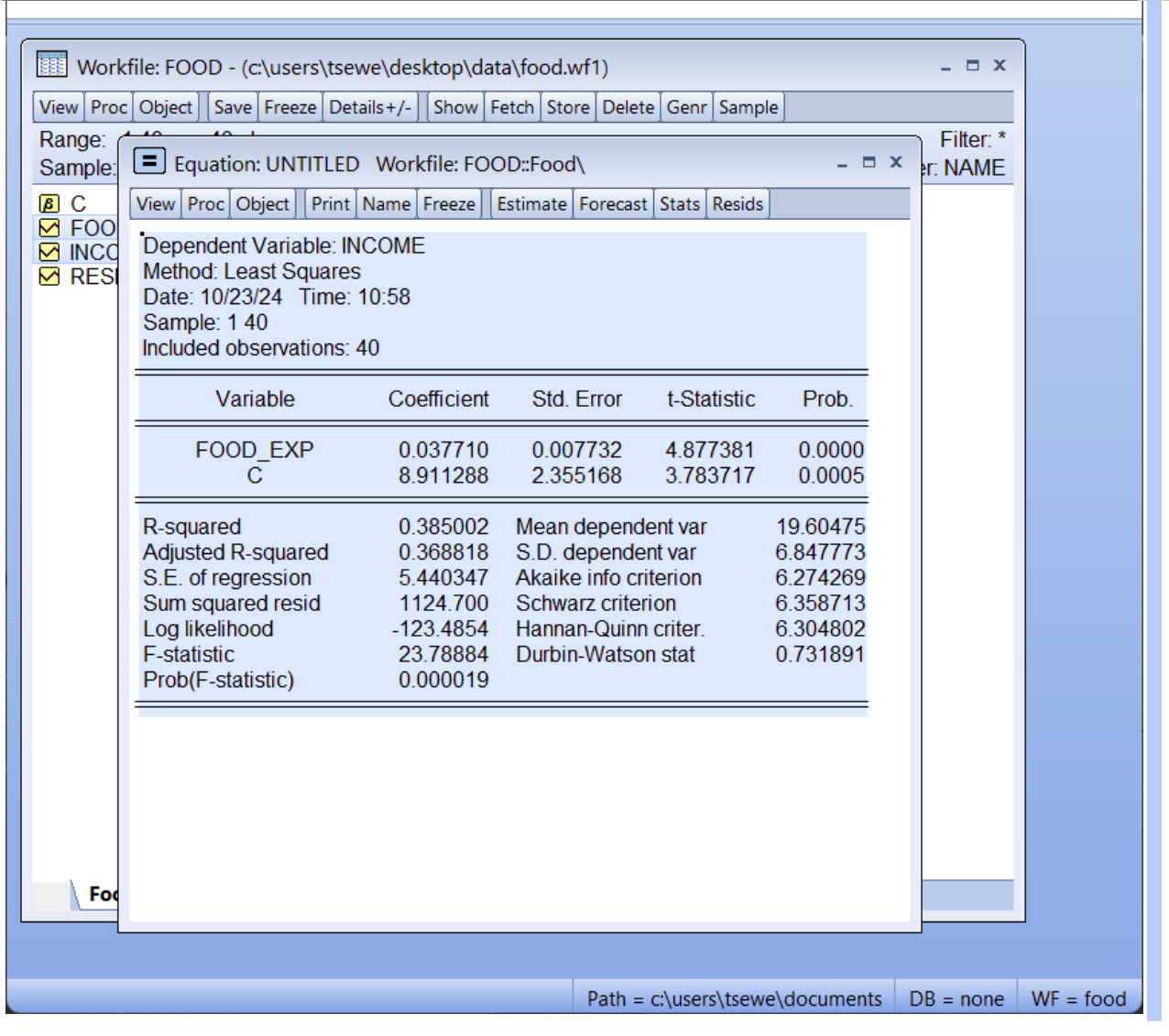
變數和係數
• INCOME: 這是收入的係數,值為
10.20964。這意味著收入每增加一個單位,食品支出預計增加約 10.21
單位。
• C: 這是截距項,值為
83.41600。這表示當收入為零時,食品支出的預測值為 83.41600。
標準誤 Std. Error
• INCOME: 標準誤為
2.093264,表示係數估計的精確度。較小的標準誤表示估計值較為精確。
•
C: 截距項的標準誤為 43.41016。
t-統計量
t-Statistic
• INCOME: t-統計量為
4.877381,用來檢驗係數是否顯著。一般來說,t-統計量的絕對值大於 2
表示係數顯著。
• C: 截距項的 t-統計量為 1.921578。
p-值(Prob.)
• INCOME: p-值為
0.0000,表示係數在統計上顯著,意味著收入對食品支出有顯著影響。
• C:
截距項的 p-值為 0.0622,接近於顯著水平(通常為
0.05),但不完全顯著。
R 平方(R-squared)
• R-squared:
值為 0.385002,表示模型解釋了約 38.5%
的食品支出變異。這是一個衡量模型擬合優度的指標。
調整後的 R平方(Adjusted R-squared)
• Adjusted R-squared: 值為0.368818,調整後的 R平方考慮了模型中的變數數量,提供了一個更保守的擬合優度評估。
標準誤
S.E. of regression
• S.E. of regression: 值為89.51700,表示回歸模型的標準誤差。
殘差平方和(Sum squaredresid)
• Sum squared resid: 值為304505.2,表示殘差的平方和,用於衡量模型的擬合程度。
信息準則 Akaike info criterion, Schwarz criterion, Hannan-Quinn criter.
• Akaike info criterion (AIC): 值為 11.87544。
• Schwarz criterion (SC): 值為 11.95988。
• Hannan-Quinn criterion (HQ): 值為 11.90597。
這些信息準則用於模型選擇,較小的值表示模型更好。
F-統計量 F-statistic
• F-statistic: 值為 23.78884,用於檢驗整體模型的顯著性。較大的 F 值表示模型顯著。
• Prob(F-statistic): 值為 0.000019,表示模型在統計上顯著。
Durbin-Watson 杜賓-瓦森統計量 Durbin-Watson stat
• Durbin-Watson stat: 值為 1.893880,用於檢驗殘差的自相關性。值接近 2 表示無自相關,值遠離 2 表示存在自相關。
這些統計量共同幫助你評估回歸模型的擬合度和變數的顯著性。
W08 The multiple regression model (1)
2024-10-30-Wednesday 14:10-17:00 林師模教授
老師的講義 Ch-03 | 教科書內容 Chapter-03 | GoogleDOc 中譯 區間估計和假設檢定 Interval Estimation and Hypothesis Testing |
有兩題
3.21 The capital asset pricing model (CAPM) is described in Exercise 2.16. Use all available observations in the data file capm5 for this exercise.
3.27 Is the relationship between experience and wages constant over one’s lifetime? (使用Dataset: cps5_small)
找windows命令欄看 Eviews 5 主菜单简介
point estimates -> Interval Estimation
-c1 <= b2 <= c1
sometime we would like to have a range of b1 and b2
as to b2
1.standize b2 use fomula of Z standalization = b2-beta2 / sqr.sigma2/Sum(xi[xbar)2
P(-1.96 <= Z <= 1.96) = 0.95
根據上面公式代換Z 然後
rearange可以得出 看相片 (可以自己導看看)
問: (0.95)的Z
值範圍怎樣求出來? 練習;
如果改為0.99 怎樣算beta2?
“C:(CYCU)
Getting Started.pdf”
2)NUll hy alternative
3)test statistic
4)alpha significant level
5)conclude cretical value
現在 yi=beta1 + beta2 x + ei
important thins is: is beta2 are 0 or not! 若是0 x y就沒有關係
t 和 Z 不同只在 sigama 的hat 因為t 是sample所以是用 sigma hat
注意: 通常設 H0: beta2 = 0 H1L beta2 > 0 one tail
因為 n-2 是 40-2 這個是 右尾 要查t表
如果是two tail alph1=5% 那每邊是2.5%
也是查t表
接下來做例題練習
p123 Exam 3.4 Examples of Hypothesis
Tests
what is difination of p-vale
- The p-value (or probability value)
is a measure used in statistical hypothesis testing to determine the
significance of the results. It represents the probability of obtaining
test results at least as extreme as the observed results, assuming that
the null hypothesis is truehttps://en.wikipedia.org/wiki/P-value
- 算出來是6% p-value, 但設定的rejection area是5% 所以 no-reject (not
be albe to reject)
- 要注意是雙尾 還是單尾。若是雙尾, p-value%就要x2
(EViews通常設定是給雙尾,如果你要單尾 要自己 /2)
請看p.123 的5說明 你用tvalue 去判斷也可以 換成用p-value去判斷也ok
再看Right Taile的測試案例 EXAMPLE 3.3 Right-Tail Test of an Economic
Hypothesis
注意 t值>critical value才可以reject.
這幾個例題都要自己重新做過
- 通常alternative是你相信的
null是你想reject的
EViews的公式: c(2) 表示請計算 coefficent 第2個
(b2)
請看相片 跑出來的Probability 如果設定是0.01的話,
因為是單尾,所以0.03要/2 為-.015 所以 not reject
每個星期三下午都是頭腦體操時間,本來好不容易弄懂的東西,被幾個例題加上兩張表(t-value,
p-value)又弄得七葷八素,頭暈眼花。
(看)課本: Principles of
Econometrics, 5th Edition
今天從p.112的 CHAPTER 3
開始講,因為講完問any question時大多沒人問(還在迷糊中),老師就說OK then
we moveon …或是the next one 這樣例題做得越多 問題越多
第三個小時竟然要講last part of Chp.3了 三小時講完1個chapter
(p.112-151共40頁)
- 老師隨時可以拿出一個 變異數的公式
把各種var()換來換去
-
如果用software如EViews他通常把這些數字都丟給你取用
談到課本有小錯誤 2.024才對
通常H0: beta2 = 0 可作 t test (single test, only one constrain, only
one mean)
此時 t 和 F test 是一樣的 兩個都可以做 F=t^2
若是join
test H0: beta1 = beta2 = 0 是用F test
(one equal sign is one
constrain)
但有時會這樣 H0: beta1 + 2 beta2 = 0 怎辦?
因為只有一個eaual
所以也是用t test
把(beta1 + 2beta2) 看成一個lenear combination
要去查review
stastics
看例題3.6
3.7 注意原來income是100所以 現在問的是2000所以 要改為
20 個 unit income
- 此外這裡要用到第三章開始的interval 公式 p( b2-… beta2 …) 原來公式是
beta2 但現在是要找 expenditure所以改為要找(beta1 + beta2 * 20)
這樣!就要接到Example 3.8的解釋了
接下來要demo怎樣用EViews做出這些結果
因為只想要Std. err所以
function
c(1) + c(2) 20 = 0,1,2…. 都沒差. std.err都一樣!!!!
最後 EXAMP LE 3.6 (continued) p-Value for a Two-Tail Test of
Significance
XAMPLE 3.9 Testing Expected Food
Expenditure
Assignment2:
-p.140- 3.21 data set is called capm5 answer 5
questions
-p.142- 3.27 data set cps5 answer 5 questions
-assignments requiered, No more than 2 pages,
AI來幫忙: 我在讀Principles of Econometrics, 5th Edition (Wiley)
這本書,其中有個的題目如下,請解釋這個題目的內容
在 EViews
軟體中,模型設定語法中的 C 是一個預定義的係數向量。具體來說,C
通常用來表示截距項或常數項。在回歸模型中,C
代表模型中的常數項,這樣你就不需要手動定義每個模型的截距。
例如,在
EViews 中設置一個簡單的線性回歸模型時,你可能會看到如下語法:
equation eq1.ls y c x1 x2
在這裡,c 代表截距項,x1 和 x2
是自變量。
C 是 EViews
中的一個保留字,這意味著它在軟體內部有特定的用途和定義,並且不能用作其他變量名稱
Problems with
“C” (constant) t is nothing to worry about. C is always exactly the
same size in all workfiles.。
李宗璋老師講Eviews
1
Eviews
3 绘制散点图
views
4 估计回归方程
Eviews
5 主菜单简介
李宗璋老師講Eviews
1暨南大學統計學碩士,華南理工大學管理學博士,現任教於華南農業大學經濟管理學院。
Eviews实战与数据分析(新时代·技术新未来)
https://item.jd.com/14260514.html
@申請EViews12 學生版..
作者:
李宗璋老師Eviews實戰與數據分析
AHP
階層分析概論(二)
- 參考案例
你可以參考一些績效考核的實例來了解更多細節,例如H&L Management
Consultants的
- 績效考核指標和流程,以及
國立陽明交通大學的AHP法應用
a。
第一章第03讲 层次分析法案例分析
GoogleSheet AHP練習
有購車與N2的Sales評分例題。
GoogleSheet AHP_考核表
202411想要用AHP做業務soft排行。
@還要做CI一致性檢定 Consistency
Index一致性指標CI (W12)有一表格不在0.1以下,此問卷就無效。
每個成對比較都要有CI 和CR值 (RI是查表得到的 CI是計算出來的)
RI是平均的CI值
AI來幫忙: 做層級分析AHP時,為什麼需要求CI
和CR值,有什麼作用?要怎樣計算?
謝謝,請你重做「我的部門有5個業務員,請問可以用AHP法,評估他們在工作態度、溝通能力、專業知識、團隊精神(設此四項為等權重)的得分,然後予以排名嗎?要怎樣做?有沒有類似的案例可供參考?」並在說明中計算CI
和CR值,並進行解釋。
< brERi = Rf + βi(ERm−Rf) < br<br 其中:<br • ERi 是投資的預期回報率<br • Rf 是無風險利率(通常是國庫券利率)<br • βi 是投資的貝塔值,表示該資產相對於市場的波動性<br • (ERm−Rf) 是市場風險溢價,即市場的預期回報率減去無風險利率<br CAPM 的核心思想是,投資者應該獲得與其承擔的風險相對應的回報。這個模型廣泛應用於金融領域,用於定價風險資產和生成資產的預期回報率。<br Capital Asset Pricing Model (CAPM): Definition, Formula, and Assumptions <br Capital Asset Pricing Model (CAPM) <br What is a capital asset pricing model? <br
W09 Mid-term report
2024-11-06-Wednesday 14:10-17:00 林師模教授
- 期中考週,本日不上課。
- 請完成作業Assignment2
W10 The multiple regression model (2)
2024-11-13-Wednesday 14:10-17:00 林師模教授
老師的講義 Ch-04 | 教科書內容 Chapter-04 | GoogleDOc 中譯 區間估計和假設檢定 Interval Estimation and Hypothesis Testing |
sensitive lever
high volidality = high risk
r = Pt-P(t-1) / P(t-1)
- 老師問: 請看alfa value (c(1))的 pvalue:
What is the meaning of intecpt significant or insignificant?
if it is insignificant? does that mean
因為c1 理論上不存在 所以pvalue >0.05 是insignificant 合理,萬一發生
significant時如何解釋,解釋是: 可能這個股票發生 有了 extra return!!
3.27
- 為了easy to handle the equation, we generate a new
variable exper30
series exper30=exper-30
- 老師問 queation b, we
found that c(2) is <0 , what is that mean?
y = c1 +c2 x^2 + e
slope = dy/dx = 2 * C2 * x (記住這個公式) =
解釋: x: exper30
所以這個數字 有些正 有些負 所以當 c2 是負數,
結果就會是有些正有些負(因為exper30 = x = 有些正有些負)
- c 先用focast 做出 wagef, 再取exper30 wagef
做group-grah-scater
- Ho: beta=0 test the significant is trying to derermin that wheter
dependent and independent variable has relationship or not.
Excep that we can try to find
“How fit are the obs to the regression line?” - 只要掌握SSE 就可以算出R square
Pusaka Monkawan soro,
- r(xy) = Cov(x,y)/ sqr.Var(x) * sqr.Var(y) and R square = r(xy)^2
- R square = r(y yhar)^2
看課本4.2
去forcate 找出predict value of food_ependf
驗算(看相片)證明了4.2.2 的公式 和 p,158最後2.這段所說Example 4.3 通常做完後 會把equation列出
這個例子 列出(se) 也可以列出 t-value (因為列出se也可以算出t) 後面列出是significance level 10% 5% 1%的意思
像這個pvalue 是 0.0622 那只有在10%時是significent
用 10.21/2.09 就可以得到 t-value (要想一想) beta/se然後再說 R square是多少
(如果你沒放* ** 那通常你要提供 N 或 df)
4.3.1 如果你改變x的單位 beta會改變 比如原來是dollar 變為hundred dollar.
注意看(c beta)(x/c) 如果x 除以一個constant c 那麼beta 那裡也要乘一個c 才可抵銷
這樣就會引起beta 值改變為新的(c beta)值
4.2.2 萬一如果是y的單位改了
4.3.2 Choosing a Functional Form
- unit變了coefficent和se會變,但
t,p vale 和R square 不會變
- reflection point 如果quadratic是1個
cubic是2個
- 如果你看到scater polot 是幾個reflection point
你要選擇相應的equation
plot the x and y first, to decide what is the
funtion more suitable.
像e和f 是log for y 和log for x 的不同 (ln log
natural)
請看p.163- Table 4.1 Some Useful Functions, Their Derivatives,
Elasticities, and Other Interpretation
注意slope 和 Elasticity
的不同
每星期三的課是最有趣的,也是最頭痛的,每次聽到下半節,都希望老師趕快停止,不然腦袋裝不下。
老師也會把公式背錯(講錯),直到看課本的例題解釋時才想到(發現),趕快回去改黑板。我很多都是用照相的,稍不小心會照到錯的,錯過改正的。那就慘了。
有個log-log的公式,老師問說這個很簡單,那一位同學可以上來黑板,寫出答案來。
大家推來推去,沒人上去。
我等著老師講解,回去再重新看對數運算。上個月才看過,現在都忘光了。
對數
看影片 老師有演算過程.
4.1 Least Squares Prediction
4.2 Measuring
Goodness-of-Fit
4.3 Modeling Issues
4.4 Polynomial
Models
4.5 Log-Linear Models
4.6 Log-Log Models
用Python做Regression Analysis
spyder phthon 3.9
Linear Regression) #2
Python實作 by 國立屏東大學林彥廷老師
機器學習(Machine
Learning) - 簡單線性回歸(Simple Linear Regression) #3 Python實作 by
國立屏東大學林彥廷老師
機器學習(Machine
Learning) - 簡單線性回歸(Simple Linear Regression) #4 Python實作 by
國立屏東大學林彥廷老師
中国大学MOOC-慕课
陳磊老師 1
1 1计量经济学概述
模型設定
1.4
1 1遗漏变量与不相干变量 14:13
2.4
1 2模型设定准则 15:51
3.4
2 1函数形式的选择 12:30
AI幫忙: 請將 “EXAMPLE 4.13 A Log-Log Poultry Demand Equation”
的內容,翻譯成中文,並解釋其意思。
4.3.2 Choosing a Functional Form
p.162 有6種models的圖形
p.162 Table 4.1 Some Useful Functions, Their Derivatives, Elasticities,
and Other Interpretation
有6種models的圖形
4.3.3 A Linear-Log
Food Expenditure Model
這是一個例題 EXAMPLE 4.13 A Log-Log Poultry Demand
Equation
例 4.13 對數-對數家禽需求方程 (內容如下)
The
log-log functional form is frequently used for demand equations.
Consider, for example, the demand for edible chicken, which the U.S.
Department of Agriculture calls “broilers.” The data for this exercise
are in the data file newbroiler, which is adapted from the data provided
by Epple and McCallum (2006).2 The scatter plot of
Q = per capita consumption of chicken, in pounds, versus
P = real
price of chicken is shown in Figure 4.15 for 52 annual observations,
1950–2001.
It shows the characteristic hyperbolic shape that was displayed in
Figure 4.5(d). The estimated log-log model is
ln(Q)⋀= 3.717 − 1.121
× ln(P) R2
g = 0.8817 (4.15)
(se) (0.022) (0.049)
We estimate that the price elasticity of demand is 1.121: a 1% increase
in real price is estimated to reduce quantity consumed by 1.121%.
point estimates -> Interval Estimation
-c1 <= b2 <= c1
sometime we would like to have a range of b1 and b2
as to b2
1.standize b2 use fomula of Z standalization = b2-beta2 / sqr.sigma2/Sum(xi[xbar)2
P(-1.96 <= Z <= 1.96) = 0.95
根據上面公式代換Z 然後
rearange可以得出 看相片 (可以自己導看看)
問: (0.95)的Z
值範圍怎樣求出來? 練習;
如果改為0.99 怎樣算beta2?
“C:(CYCU)
Getting Started.pdf”
2.
1)Question
2)NUll hy
alternative
3)test statistic
4)alpha significant level
5)conclude cretical value
現在 yi=beta1 + beta2 x + ei
important thins is: is beta2 are 0 or not! 若是0 x y就沒有關係
t 和
Z 不同只在 sigama 的hat 因為t 是sample所以是用 sigma hat
注意:
通常設 H0: beta2 = 0 H1L beta2 > 0 one tail
因為 n-2 是 40-2
這個是 右尾 要查t表
如果是two tail alph1=5% 那每邊是2.5%
也是查t表
接下來做例題練習
p123 Exam 3.4 Examples of Hypothesis
Tests
what is difination of p-vale
- The p-value (or probability value)
is a measure used in statistical hypothesis testing to determine the
significance of the results. It represents the probability of obtaining
test results at least as extreme as the observed results, assuming that
the null hypothesis is truehttps://en.wikipedia.org/wiki/P-value
- 算出來是6% p-value, 但設定的rejection area是5% 所以 no-reject (not
be albe to reject)
- 要注意是雙尾 還是單尾。若是雙尾, p-value%就要x2
(EViews通常設定是給雙尾,如果你要單尾 要自己 /2)
請看p.123 的5說明 你用tvalue 去判斷也可以 換成用p-value去判斷也ok
再看Right Taile的測試案例 EXAMPLE 3.3 Right-Tail Test of an Economic
Hypothesis
注意 t值>critical value才可以reject.
這幾個例題都要自己重新做過
- 通常alternative是你相信的
null是你想reject的
EViews的公式: c(2) 表示請計算 coefficent 第2個
(b2)
請看相片 跑出來的Probability 如果設定是0.01的話,
因為是單尾,所以0.03要/2 為-.015 所以 not reject
每個星期三下午都是頭腦體操時間,本來好不容易弄懂的東西,被幾個例題加上兩張表(t-value,
p-value)又弄得七葷八素,頭暈眼花。
(看)課本: Principles of
Econometrics, 5th Edition
今天從p.112的 CHAPTER 3
開始講,因為講完問any question時大多沒人問(還在迷糊中),老師就說OK then
we moveon …或是the next one 這樣例題做得越多 問題越多
第三個小時竟然要講last part of Chp.3了 三小時講完1個chapter
(p.112-151共40頁)
- 老師隨時可以拿出一個 變異數的公式
把各種var()換來換去
-
如果用software如EViews他通常把這些數字都丟給你取用
談到課本有小錯誤 2.024才對
通常H0: beta2 = 0 可作 t test (single test, only one constrain, only
one mean)
此時 t 和 F test 是一樣的 兩個都可以做 F=t^2
若是join
test H0: beta1 = beta2 = 0 是用F test
(one equal sign is one
constrain)
但有時會這樣 H0: beta1 + 2 beta2 = 0 怎辦?
因為只有一個eaual
所以也是用t test
把(beta1 + 2beta2) 看成一個lenear combination
要去查review
stastics
看例題3.6
3.7 注意原來income是100所以 現在問的是2000所以 要改為
20 個 unit income
- 此外這裡要用到第三章開始的interval 公式 p( b2-… beta2 …) 原來公式是
beta2 但現在是要找 expenditure所以改為要找(beta1 + beta2 * 20)
這樣!就要接到Example 3.8的解釋了
接下來要demo怎樣用EViews做出這些結果
因為只想要Std. err所以
function
c(1) + c(2) 20 = 0,1,2…. 都沒差. std.err都一樣!!!!
最後 EXAMP LE 3.6 (continued) p-Value for a Two-Tail Test of
Significance
XAMPLE 3.9 Testing Expected Food
Expenditure
Assignment2:
-p.140- 3.21 data set is called capm5 answer 5
questions
-p.142- 3.27 data set cps5 answer 5 questions
-assignments requiered, No more than 2 pages,
AI來幫忙: 我在讀Principles of Econometrics, 5th Edition (Wiley)
這本書,其中有個的題目如下,請解釋這個題目的內容
在 EViews
軟體中,模型設定語法中的 C 是一個預定義的係數向量。具體來說,C
通常用來表示截距項或常數項。在回歸模型中,C
代表模型中的常數項,這樣你就不需要手動定義每個模型的截距。
例如,在
EViews 中設置一個簡單的線性回歸模型時,你可能會看到如下語法:
equation eq1.ls y c x1 x2
在這裡,c 代表截距項,x1 和 x2
是自變量。
C 是 EViews
中的一個保留字,這意味著它在軟體內部有特定的用途和定義,並且不能用作其他變量名稱
Problems with
“C” (constant) t is nothing to worry about. C is always exactly the
same size in all workfiles.。
李宗璋老師講Eviews
1
Eviews
3 绘制散点图
views
4 估计回归方程
Eviews
5 主菜单简介
李宗璋老師講Eviews
1暨南大學統計學碩士,華南理工大學管理學博士,現任教於華南農業大學經濟管理學院。
Eviews实战与数据分析(新时代·技术新未来)
https://item.jd.com/14260514.html
@申請EViews12 學生版..
作者:
李宗璋老師Eviews實戰與數據分析
AHP
階層分析概論(二)
- 參考案例
你可以參考一些績效考核的實例來了解更多細節,例如H&L Management
Consultants的
- 績效考核指標和流程,以及
國立陽明交通大學的AHP法應用
a。
第一章第03讲 层次分析法案例分析
GoogleSheet AHP練習
有購車與N2的Sales評分例題。
GoogleSheet AHP_考核表
202411想要用AHP做業務soft排行。
@還要做CI一致性檢定 Consistency
Index一致性指標CI (W12)有一表格不在0.1以下,此問卷就無效。
每個成對比較都要有CI 和CR值 (RI是查表得到的 CI是計算出來的)
RI是平均的CI值
AI來幫忙: 做層級分析AHP時,為什麼需要求CI
和CR值,有什麼作用?要怎樣計算?
謝謝,請你重做「我的部門有5個業務員,請問可以用AHP法,評估他們在工作態度、溝通能力、專業知識、團隊精神(設此四項為等權重)的得分,然後予以排名嗎?要怎樣做?有沒有類似的案例可供參考?」並在說明中計算CI
和CR值,並進行解釋。
< brERi = Rf + βi(ERm−Rf) < br<br 其中:<br • ERi 是投資的預期回報率<br • Rf 是無風險利率(通常是國庫券利率)<br • βi 是投資的貝塔值,表示該資產相對於市場的波動性<br • (ERm−Rf) 是市場風險溢價,即市場的預期回報率減去無風險利率<br CAPM 的核心思想是,投資者應該獲得與其承擔的風險相對應的回報。這個模型廣泛應用於金融領域,用於定價風險資產和生成資產的預期回報率。<br Capital Asset Pricing Model (CAPM): Definition, Formula, and Assumptions <br Capital Asset Pricing Model (CAPM) <br What is a capital asset pricing model? <br
eσ̂ 2∕2= exp(3.717 − 1.121 × ln(P))
e0.0139∕2
陳磊的課.md
W11 Further inference in multiple regression model
2024-11-20-Wednesday 14:10-17:00 林師模教授
老師的講義 Ch-04 | 教科書內容 Chapter-04 | GoogleDOc 中譯 區間估計和假設檢定 Interval Estimation and Hypothesis Testing |
2024/1120課前預習
- 這是Chapter的各章節介紹
Based on the material in this chapter, you should be able to
Explain how to use the simple linear regression model to predict the value of y for a given value of x.
Explain, intuitively and technically, why predictions for x values further from x are less reliable.
Explain the meaning of SST, SSR, and SSE, and how they are related to R2.
Define and explain the meaning of the coefficient of determination.
Explain the relationship between correlation analysis and R2.
Report the results of a fitted regression equation in such a way that confidence intervals and hypothesis tests for the unknown coefficients can be constructed quickly and easily.
Describe how estimated coefficients and other quantities from a regression equation will change when the variables are scaled. Why would you want to scale the variables?
Appreciate the wide range of nonlinear functions that can be estimated using a model that is linear in the parameters.
Write down the equations for the log-log, log-linear, and linear-log functional forms.
Explain the difference between the slope of a functional form and the elasticity from a functional form.
Explain how you would go about choosing a functional form and deciding that a functional form is adequate.
Explain how to test whether the equation ‘‘errors’’ are normally distributed.
Explain how to compute a prediction, a prediction interval, and a goodness-of-fit measure in a log-linear model.
Explain alternative methods for detecting unusual, extreme, or incorrect data values.
1.貝葉斯定理/條件機率 複習
貝氏估計法貝氏定理:
P(A)P(B|A)=P(B)P(A|B)
2.指數與對數運算
1).指數與對數內有9個課程。
4).自然對數
5).指數函數之微分
6).對數函數的微分
(沒時間做)3.微分與偏導數; 4.Chapter4練習題-EViews應用; 5.AIC與;
統計學-李柏堅-第15章-點估計(二)
貝氏估計法事前與事後機率。
貝氏估計法應用於醫學檢驗
Unbiasedness 不偏估計量
Efficiency 有效估計量
onsistency 一致估計量
Sufficiency 充分估計量
歷屆考題賞析(最大概似估計量)
歷屆考題賞析(不偏估計量)
2024/1120筆記
EViews的equation estimate寫y=β1+β2 ln(x)這行function的command:y c log(x)
所以food.wf我用 food_exp c log(income) 就可以了
老師的講義4.2.1有公式: Syy Sx Sy rxy^2 = R^2
4.3.1 The Effects of Scaling the Data 縮放資料的影響
老師從p.163 Some Useful Functions, Their Derivatives, Elasticities, and Other Interpretation的Log-Log的推導講起: 算為什麼Slope和Elasticity是這樣。
以下其他推導derive請自行計算slope和exlaticity (從公式導出)
Log-linear model 注意:
or, a 1-unit change in x leads to (approximately) a 100β2% change in y
Liner-Log model 注意:
or, a 1% change in x leads to (approximately) a β2∕100 unit change in yExample 4.3.3 我們原來設定這個model是 linear model現在我們做這個是 Linear-log model
如果delta x有1%變化….看EXAMPLE 4.4
如果1% change in income 會有123.17 /100 = 1.2317 change in y(food_exp)
下面解釋:如果週薪增加了1000元,會多花13.22元在食物消費
解釋中讓你比較兩種模型的結果 linear-log 和 linear-linear
估算每增100元收入 會增加多食物支出注意Remark: 最重要是參考經濟理論-其次再參考emperical data如果和理論有違誤應該試著換model再試看看
這部份可參考陳磊-4 2 1函数形式的选择接下來要討論4.3.4 Using Diagnostic Result Plot 我們最歡迎(a)random residule 且mean=0 這種散佈圖,是good sign。
圖(b) residule is incresing 可能equation 有點問題,雖然mean=0
(c)(d)和(b)都類似 只是他是decresing和increasing的變化。
像fig 4.8,觀察fit的情況,如果表現不好,或還有改進空間。可以換個model再觀察residule圖看看。注意p.168 The Jarque–Bera statistic : 這是觀察Skewness and ktosis的情況的
會看出: Skewness indicates the degree of tilt in data,
一般而言,為了表示樣本所由來之族群分布與常態分布(normal distribution)偏離的情況,通常會使用歪度(skewness)跟峯度(kurtosis)這兩種統計值,而歪度係數(coefficient of skewness)跟峯度係數(coefficient of kurtosis)的計算牽涉到前四級動差( ..
如果JB is big then we will reject Null Hypo??(這段待看課文,核對確否)
比如run regression 後check residule 如果 JB 0.063340 因p.169有說明critical value,所以就可以-拿JB值和critical value做比較。練習EViews > 用residul < 作圖 >
normality常態 would be the minor one to look at, is it important or not.
EXAMPLE 4.8 An Empirical Example of a Cubic Equation
像是total cost就可能用到cubic好, similar situation like utility.
在economic上有很多example可以參考
在4.5 是Log-linear model有 EXAMPLE 4.9 Growth model
(we_wheat.wf)看 0.0178t 因為t是independent 而0.0178是b2 就是 growth rate
log(greenough) c time
greenough c time^3 focast name it as g3 (存成object)
後把幾個通通group起來 view -graph -scater plotEXAMPLE 4.10 A Wage Equation 這是研究return on school time!的例子。
根據結果 0.0988 EDUC
如果你有1 unit increase (多讀了1年) 你的薪水會增加 9.9%EXAMPLE 4.13 A Log-Log Poultry Demand Equation 家禽需求方程
We estimate that the price elasticity of demand is 1.121: a 1%
increase in real price is estimated to reduce quantity consumed by 1.121%. quantity demand (comsumption) 所以quantity demand 對價格變化很敏感。有人問: money vs. time 的model 老師說=> 比如一樣錢 10年前後購買力不同 要考慮 通膨,利率 等變數
- 4.29 Consider a model for household expenditure as a function of household income using the 2013 data from the Consumer Expenditure Survey, cex5_small. The data file cex5 contains more observations.
Our attention is restricted to three-person households, consisting of a husband, a wife, plus one other.
In this exercise, we examine expenditures on a staple item, food. In this extended example, you are asked to compare the linear, log-log, and linear-log specifications.
a. Calculate summary statistics for the variables: FOOD and INCOME. Report for each the sample mean, median, minimum, maximum, and standard deviation. Construct histograms for both variables. Locate the variable mean and median on each histogram. Are the histograms symmetrical and “bell-shaped” curves? Is the sample mean larger than the median, or vice versa? Carry out the Jarque–Bera test for the normality of each variable.
b. Estimate the linear relationship FOOD = β1 + β2 INCOME + e. Create a scatter plot FOOD versus INCOME and include the fitted least squares line. Construct a 95% interval estimate for β2. Have we estimated the effect of changing income on average FOOD relatively precisely, or not?
c. Obtain the least squares residuals from the regression in (b) and plot them against INCOME. Do you observe any patterns? Construct a residual histogram and carry out the Jarque–Bera test for normality. Is it more important for the variables FOOD and INCOME to be normally distributed, or that the random error e be normally distributed? Explain your reasoning.
d. Calculate both a point estimate and a 95% interval estimate of the elasticity of food expenditure with respect to income at INCOME = 19, 65, and 160, and the corresponding points on the fitted line, which you may treat as not random. Are the estimated elasticities similar or dissimilar? Do the interval estimates overlap or not? As INCOME increases should the income elasticity for food increase or decrease, based on Economics principles?
e. For expenditures on food, estimate the log-log relationship ln(FOOD) = γ1 + γ2 ln(INCOME) + e. Create a scatter plot for ln(FOOD) versus ln(INCOME) and include the fitted least squares line. Compare this to the plot in (b). Is the relationship more or less well-defined for the log-log model relative to the linear specification? Calculate the generalized R2 for the log-log model and compare it to the R2 from the linear model. Which of the models seems to fit the data better?
f. Construct a point and 95% interval estimate of the elasticity for the log-log model. Is the elasticity of food expenditure from the log-log model similar to that in part (d), or dissimilar? Provide statistical evidence for your claim.
g. Obtain the least squares residuals from the log-log model and plot them against ln(INCOME). Do you observe any patterns? Construct a residual histogram and carry out the Jarque–Bera test for normality. What do you conclude about the normality of the regression errors in this model?
h. For expenditures on food, estimate the linear-log relationship FOOD = α1 + α2 ln(INCOME) + e. Create a scatter plot for FOOD versus ln(INCOME) and include the fitted least squares line. Compare this to the plots in (b) and (e). Is this relationship more well-defined compared to the others? Compare the R2 values. Which of the models seems to fit the data better?
i. Construct a point and 95% interval estimate of the elasticity for the linear-log model at INCOME = 19, 65, and 160, and the corresponding points on the fitted line, which you may treat as not random. Is the elasticity of food expenditure similar to those from the other models, or dissimilar? Provide statistical evidence for your claim.
j. Obtain the least squares residuals from the linear-log model and plot them against ln(INCOME). Do you observe any patterns? Construct a residual histogram and carry out the Jarque–Bera test for normality. What do you conclude about the normality of the regression errors in this model?
k. Based on this exercise, do you prefer the linear relationship model, or the log-log model or the linear-log model? Explain your reasoning.
下週要開始講Chapter 5: Multiple regression model
W12 Further inference in multiple regression model
2024-11-27-Wednesday 14:10-17:00 林師模教授
老師的講義 Ch-05 | 教科書內容 Chapter-05 | GoogleDOc 中譯 The Multiple Regression Model | 多元回歸模型 (重回歸)
2024/1127課前預習
- 這是Chapter 5 的各章節介紹
Based on the material in this chapter, you should be able to
- Recognize a multiple regression model and be able to interpret the coefficients in that model.
- Understand and explain the meanings of the assumptions for the multiple regression model.
- Use your computer to find least squares estimates of the coefficients in a multiple regression model, and interpret those estimates.
- Explain the meaning of the Gauss–Markov theorem.
- Compute and explain the meaning of R2 in a multiple regression model.
- Explain the Frisch–Waugh–Lovell Theorem and estimate examples to show how it works.
- Use your computer to obtain variance and covariance estimates, and standard errors, for the estimated coefficients in a multiple regression model.
- Explain the circumstances under which coefficient variances (and standard errors) are likely to be relatively high, and those under which they are likely to be relatively low.
- Find interval estimates for single coefficients and linear combinations of coefficients, and interpret the interval estimates.
- Test hypotheses about single coefficients and about linear combinations of coefficients in a multiple regression model. In particular, a. What is the difference between a one-tail and a two-tail test? b. How do you compute the p-value for a one-tail test, and for a two-tail test? c. What is meant by ‘‘testing the significance of a coefficient’’? d. What is the meaning of the t-values and p-values that appear in your computer output? e. How do you compute the standard error of a linear combination of coefficient estimates?
- Estimate and interpret multiple regression models with polynomial and interaction variables.
- Find point and interval estimates and test hypotheses for marginal effects in polynomial regressions and models with interaction variables.
- Explain the difference between finite and large sample properties of an estimator.
- Explain what is meant by consistency and asymptotic normality.
- Describe the circumstances under which we can use the finite sample properties of the least squares estimator, and the circumstances under which asymptotic properties are required.
- Use your computer to compute the standard error of a nonlinear function of estimators. Use that standard error to find interval estimates and to test hypotheses about nonlinear functions of coefficients.
2024/1127筆記
advertising amounts:
demand is price-inelastic -> 需求是價格無彈性的 =reduction in
price leads only to a small increase in the quantity sold, sales revenue
will fall.
demand is price-elastic = a price reduction that leads to
a large increase in quantity sold will produce an increase in
revenue.
至關重要: This economic information is essential for
effective management. The economic model is:
SALES = β1 + β2 PRICE
+ β3 ADVERT
Thousands of dollars, Same city, Mothly figure.
some kind of average price -> constructed a single price index PRICE measured in dollars and cents, that describes overall prices in each city.
To be more precise about the interpretation of these parameters, we move from the economic model in (5.1) to an econometric model that makes explicit assumptions about the way the data are generated. 為了更準確地解釋這些參數,我們從(5.1)中的經濟模型轉向計量經濟模型,該模型對資料的產生方式做出明確的假設。
5.1.1 The Economic Model 1 of 2
The model is: multiple
regression model
(5.1) SALES = β1 + β2 PRICE + β3 ADVERT
5.1.2 The Economic Model 1 of 2
(5.2)
(5.5)
β2 =
(ADVERT held constant) partial regression (because held some other)
β3 = (ADVERT held constant)
5.1.3 The General Model
5.1.4 if we companre the basic
assumption for the two model
看照片
assumption
companre the basic assumption for the Simple Regression Model and
Multiple Regression mode by markdown language in table formate
- in multiple not only one X : no exact linean relationship between
Xs
如果 x2 = 5 +3x3 這就是exact relationship 因為roa. p = 1 (corelation coefficient)
copilot20241127 y=5+3x 請問corelation coefficient of x and y
怎樣算?是多少?
★ collinearity 共線性
var(b2) = 和 multiple var(b2) 的分母不一樣 要乘一個 (1-p23^2)
什麼時候 什麼狀況 需要用到 var(b2)?
有兩個用途:
1.可以找出interval for b2, standard deviation= is just the square root of var(b2)
2,when we do tet of Ho: beta2 =0; t test 這時也須用到 b2 和 sd
★共線性 會讓p 接近1 讓 分母的 sigma square 一直放大 讓 t變小到無法 reject Ho
這是因為會讓var(b2) inflated兩者相比 就是第五項 的 共線性 的不同
df 是 n- (看有幾個x variables 加上一個 intercept)
Ho: b2=b3=0 我們做join test 時就要用 F test,
如果 Ho: b2=0 只要做 t test
見課本 p.200 講partial 微分 held price事
p.201 summary
stastic
p.202
5.1.4 講到 assumtion of model MR1-MR6
5.2.1 LSE procedure
EXAMPLE 5.2 OLS estimate
-
但一直增加廣告 業績真能一直增加嗎? 這是liner relationship的問題
TABLE 5.2 可算出t p value
- 有人問what is R^2 和 General R^2 老師說通常我們用regular 不用General
R^2
大部分情況 兩者相等。只有特殊狀況 兩者有點不同
5.2.2 要小心df (5.11 K=3)
EXAMPLE 5.3 Error variance estimate
for Hamburger Chain Data
equation sales c price advert
講到 F test 公式F = {(SSE r - SSE ur) /df1 } / SSE ur / df2
ur
un restrict
做test首先想要知道 probit.
Copiot20241127 what will be if Chi Squate divided by df
- SSEur means original model,
- apply restriction to the model call Restricted model:
beta1=beta2=0
Yi = beta 1 + e i this is SSEr 這個model 的 erro tern 會比1大 因為所有erro tern 無處去都到 e i 來了
比較(SSE r - SSE ur) big or small 可以知 variable tern
重不重要從而知道Ho 成不成立
(3115.482-1718.943 )/75-3 = 1396.539 /(n-1)-(m-3)= 1396.539/2
=698.2695
1718.943/72 = 23.874 b
F=698.2695 / 23.874 =
29.248
SSresid 1918.943
88.724/23.874=3.72 正確應該是 (7.73)= squate of
t value 2,76283
就是說如果你用F test 結果應該是 t test
的square
- 應再次研究 degree of freedom
了解到:
** 所以只要 產生兩個 model 一是原原來的 unrestricted 另一是 假設x2 或 x3為0的 restricted model 算出兩者的SSE 就可以 求出 F test value 從而判斷是否 reject Ho
b2=b3=0 的假設
** 要檢查是[否共線 ** 再者要檢查Ho是否reject
Ha是否significant
EXAMPLE 5.2.3 Error variance estimate for Humbergurg
接下來討論 Adjusted R square
R^2 = 1- SSE/SST
multiple model 增加了xi2 xi3 …. ei hat
當你增加了 xi4 xi5… ei hat
會變小 SSE變小, 所以 R^2 就會變大
看起來是better fit事實上
增加的xi不一定make sense 所以可以做adjust
改成這樣
R bar^2 = 1-
{(SSE/df )/(SST/df)} 因為當SSE因增加xi而下降時,df也下降, 所以用df
來平衡
來修正 叫做 adjusted R^2
所以multiple regression 通常看adjusted R-square不是 R square
下週要講完Chapter 5 並進入Chapter 6.
strictly exogenous 嚴格外生的; ei 沒有包含與前面xi
有共線性的變數。
∂, der, partial differentiation偏導數
請說明 4.2 Measuring Goodness-of-Fit 這一章節的內容
請說明
CHAPTER 5 The Multiple Regression Model 這一章所討論的內容
請說明
CHAPTER 6 Further Inferencein the Multiple Regression Model
這一章所討論的內容
CHAPTER 7 CHAPTER 6 Further Inferencein the
Multiple Regression Model
CHAPTER 8 Heteroskedasticity
AIC等準則,不同模型比較時,越小越好。
F檢定 H0: B1=B2=0
聯合檢定
Esitmate估計/View看結果
若在Command
window寫指令(程式)也可
殘差很重要/看Model是OK不OK:
每估完一個equation就會出現(概過去)residul 若想留下來-就用Proc>Make
Residual series 做個紀錄保留下來。
Estimation Command:
LS PRICE
C SQFT (AGE*SQFT)
Estimation Equation:
PRICE = C(1) + C(2)SQFT +
C(3)AGE*SQFT
Substituted Coefficients:
PRICE = -105.261319413 +
14.9156221016SQFT - 0.233562450215AGE*SQFT
- 若要把eq保存成物件的話用command: equation eq01.ls price c sqft
(age*sqft)
- 或這樣寫: equation eq02.ls PRICE = C(1) + C(2)SQFT +
C(3)AGE*SQFT
A
Beginner’s Guide to Collinearity: What it is and How it affects our
regression model
想說不想再學了,反正再過十幾二下來,也不知道這些跟不知道這些東西,有什麼差別 幹嘛為了這些搞不清楚的東西,累得要死!
W13 Using indicator variables (1)
2024-12-04-Wednesday 14:10-17:00 林師模教授
W14 Using indicator variables (2)
2024-12-11-Wednesday 14:10-17:00 林師模教授
老師的講義 Ch-06 | 教科書內容 Chapter-06 | GoogleDOc 中譯 The Multiple Regression Model | 多元回歸模型 (重回歸)
2024/12/11-QM
- 因為只有一個 = sign 所以可以用t test
- 要做t
test 須知 se 要知 se 就要知道 var()
- 因為只做One tail 只要看right
side 所以就決定了not be able to reject Ha 所以要同意
現在讓我們run
EViews看看andy.wfl
- 做Wakd test 打入 一個= 的 就可看到Test
Statixtic () 記得 p-value要 /2 也可看到se=0.400985
可帶入公式算看
equation是 sales c price advert advert^2
5.6 Noadvert nlineaning
relationship
if y=sales x=advert then x and y may be not learning
relationship, 曲線比較合理 y不可能x一直增加 甚至到某點 會不增甚至下降
所以不會是線性關係比較合理
- 所以如果要不同線形 可以採取不同公式
見Example 5.13 秀出各種不同
讓我們來看看 二次方的函數 quatdratic 作法
5.14 Extending the
Model for Burger Barn Sales
通常Beta4是負數 這樣當Advert大時
marginal effect(⋀ ∂SALES/∂ADVERT )會變小
When you are new to the company: education/experience/
有時需要加一個 Interaction variable 如(EDUxEXPER)
EXAMPLE 5.15
例子中有不同exper year 和 Edu 不同變化計算
EViews用 Survey data
cps5_small t
TABLE Percentage Chages in Wage
如果你是0年經驗 的新人
但受過8年教育 則你工作增加一年的話
Percentage Chages in Wage 是
3.88%
若你是受過16年教育者 則曾一年薪水增加率是2.86%
者兩個何起來就是 %WAGE/EDUC 每增一年是13.59%
- 注意 每個數字都有se
</>老師說我們跳過Skip 5.7 move on to EXAMPLE 5.17
The
Optimal level of Advertizing
怎麼算? 看圖
每次incerese = MC MR
若 MR > MC 可以繼續 Advert
若 MR < MC 不要繼續 Advert
所以tipping point 是 MR=MC 這就是 Optimal level
接下來要開始講
Chapter 6
先介紹各節 要做什麼 , 但是說6.4會skip,
其他各節下週會講,
我請Copilot再次介紹F-Test
F-test (F-Test) is a statistical
test used to compare the number of variations (ie, the degree of
dispersion of data) between two samples or multiple samples. This test
is mainly used in the following situations:
1.Comparison of variations: The F test can be used to check whether
the variations of two samples are equal. For example, when comparing two
sets of data, you can use the F test to determine whether there is a
significant difference in the number of variations between the two sets
of data.
2.Comparison of models: In regression analysis, the F test can be
used to compare different statistical models to determine which model is
more suitable for describing the data. For example, it can be used to
examine the differences between a simple linear model and a complex
model.
3.ANOVA (Analysis of Variance): The F test is very important in
analysis of variance and is used to check whether the means of multiple
groups of data are equal. This is very common in experimental designs
and multiple group comparisons.
The basic principle of the F test is to decide whether to reject the
null hypothesis by calculating the F statistic and comparing it with the
critical value. The formula for calculating the F statistic is:
F =
If the calculated F value is greater than the critical value, the
null hypothesis is rejected, indicating that there is a significant
difference in the number of variants between the two samples.
要做Wald test.前先 要做equation,然後
c(3) 2*(c4) advert =
1
規定本週作業:
Assignment4
price c sqft (sqft*age)
W15 Heteroskedasticity (1)
2024-12-18-Wednesday 14:10-17:00 林師模教授
W14的作業Asig#4 |
老師的講義 Ch-06 | 教科書內容 Chapter-06 | GoogleDOc 中譯 The Multiple Regression Model | 多元回歸模型 (重回歸)
due date of final report of QM is 10th Jan. 2025
- before we run the model we call it error term
after we estimate the mode we call it residule
EXEMPLE 6.1 Testing the Effect of Advertising
run 2 model 第一個有 beta4, 第二個沒有 beta4
求算出F value
Fc 所以要 reject NULL
用EViews跑看看 用andy.wkf
跑 wald test:
也跑一下 restricted model 看 sum square resdiul
=接下來講 6.1.1 Testing the Significance of the Model
如果做ods model
F=t^2
simple leanlier regress H0: B2=0
但multiple 時不只是 B2=0 還要其他的Bn =0
所以如果要test個別的時候 就要用Wald test
c(2)=0 你會發現這裡的 F=t^2 但和整體regression 的F不同
=自己看Summarizing the F-Test Procedure
討論 EXAMPLE 6.5 Testing
Optimal Advertising
= 1.9 這一個model是non learnliner 所以難用t test
這個例子
改用F來做test
EXAMPLE 6.6 A One-Tail Test
F-statistic of 5.74 可以核對看看
page 270的
EXAMPLE 6.8 A Nonlinear Hypothesis
天啊!才講10 page 已經問題一卡車了
因為有兩個變數相除 一看就知道是非線性關係
6.2 The Use of
Nonsample Information
就是不只 用還會用到nonsample
請看那些解釋
PB PL PR ….
為何要對所有變數取natural log 因為
Q = A *
PB(b2)PL(b2)PR(b2)*I(b2) 通常這種function
這是叫做
Cobb-Douglas, C-D function 這是非線性的
常用在
如果對這種C-D做
log
ln(Q)=ln(A)+b2 ln(PB)+b3 ln (PL)+b4 ln(PR)+b5 ln(I)
被natural log後會變成線性的
這樣就可以做least linear regression
PL是PB的替代品 酒類, PR其他的飲料, I收入也會影響到銷量Q
P是價格的意思,
如果價格加倍 收入也加倍 結果 Q 銷量應該是不變的
這樣的想法(條件) 可以impose強加(說明)我們的假設
這樣可以導出
b2+b3+b4+b5=0 這是一個nonsample information!!
選擇B4的原因是 convert
real price from ‘nominal price’
so it is real variable
這樣可以做 EXAMPLE 6.9 Restricted Least Squares
用beer.wkf 來跑看看
log(q) c log(pb/pr) log(pl/pr)
log(i/pr)
Estimation Command:
LS LOG(Q) C LOG(PB/PR) LOG(PL/PR)
LOG(I/PR)
Estimation Equation:
LOG(Q) = C(1) + C(2)LOG(PB/PR) +
C(3)LOG(PL/PR) + C(4)*LOG(I/PR)
Substituted Coefficients:
LOG(Q) = -4.79779782053 -
1.29938649251LOG(PB/PR) + 0.186815847086LOG(PL/PR) +
0.945828629933*LOG(I/PR)
作業page.309
W16 Heteroskedasticity (2)
2024-12-25-Wednesday 14:10-17:00 林師模教授
QM_期末_參考論文 The predictability of aggregate consumption growth in OECD countries: a panel data analysis
W16 12/25 Asig#5-Final Report |
老師的講義 Ch-07 | 教科書內容 Chapter-07 |
series ln_food=log(food)
series ln_income=log(income)
equation loglog_eq.ls ln_food c ln_income #建立equation
γ1=3.778932
γ2=0.186305
標準誤se=0.641762
R^2=0.033229
scalar sse = @ssr
#value是=493.406150900657
scalar sst = @sumsq(ln_food-@mean(ln_food)) #510.365152487728
scalar
r2_gen = 1 - sse/sst #0.03322915270450155
Generalized
R^=0.03322915270450155
p.271 6.2 The Use of Nonsample Information
p.272 EXAMPLE 6.9 Restricted Least Squares
今天講完chp6的下面幾節, 再講一點chp7 但可能講不完chp7
p.273 6.3 Model Specification
6.5 Poor data
6.6 nonlinear Leaset square
p.273 6.3 Model Specification
EXAMPLE 6.10 Family Income Equation
- ommited variable
想要恆量一個家庭的收入狀況,可能先考慮先生的教育程度,其次妻子的,但可能還有很多變數
這些變數有些是 缺乏資料,有些是不知如何量取資料
例(6.24)
有好幾個model比如(2) 就只取先生的教育程度變數 這樣比起(1)的b2 %大多了
也可能有bias
(3)是KL6 (小於六歲的小孩)是把小孩的加上去 會有negtive
因為會造成income流失
但你看看
沒加上妻子的,影響比加上小孩的,影響還要大。
來看個很重要的例子:
EXAMPLE 6.13 A Control Variable for
Ability
看這個model
要量取教育很容易,算年數,但要恆量ABILITY就很困難,很困難但應該是很重要的因素。
如果少了這個因素,其影響就會被歸入e (error tern)
這樣來說,比較有沒有ABILITY 的 e
因此,你可以回去看EXAMPLE 6.10
Omitted Variable Bias: A Proof T 這是第一個需要討論的問題
EXAMPLE 6.11 你自己去看看
(那些insignifcant 就是 6.33
Ierelevent variable)
接下來要討論的是
6.3.4 Control Variables
請看 EXAMPLE
6.13 A Control Variable for Ability
有時 IQ(SCIORE)
可以拿來取代ABILITY變數;
如果用這個變數,有時可以提高這個Model的精確度
proxy variables 難以恆量 但很重要的variable, cotrol variable
-
Idiris 問印尼教育的Case, 有elementry control 兩個variable.
老師說:
這裡用IQ score來取代ability是 proxy variable.
但你說的情況,是用來
控制某種情況.用的。
但這裡:
ability非常重要,但難以恆量,所以用這個proxy來取代,這兩種情況都被稱為contral
variable但作用有點不一樣。
(我就不跑EViews了 有興趣 你自己去做做看)
接下來我們討論
6.4.1 Predictive Model Selection Criteria
How many or which veriable should be included?
Yi = b1+biXi2…
解釋使用Adjusted R^2的原因
通常可以用 R^2= SSR/SST 來衡量準確性
但如果這個model被include
了irelevent 結果R^2 會加大(因為SSE會變小)
所以你如果多了一些irelevent variable但你的R^2
反而增加,所以有些研究者如果要寫paper的話
就有作弊方法(加一些沒用的varialbel)
所以multi
variate研究時。通常不看R^2而是看adjusted R^2 (考慮df的影響的)
通常R bar squae < R square (adjusted R^2 < R^2)
TAB L E 6.4 Model Selection Criteria for House Price
Example
看 增加了variable造成的Rbar squae 和 R square
比較。不管你怎樣增加variables但Rbar squae幾乎都一樣。
在這裡(看5-8
models都比1,2好) 但可能使用6,或8; 在這裡引入的(5-8)都是重要的所以Rbar
square有較大的區別。
(TABLE 6.1 正好沒有R 和 Rbar square,所以老師自己跑EViews)
像照相一樣,可以一個一個model都跑一次,記下R 和 Rbar square做比較。
加了兩個irelevent variable雖然R^2增加但 Rbar square反而下降。
AIC 和 SC都和adjueste R square很像,都是判斷variable是不是好。
AIC 和 SC越小越好。p.286 (6.43) (6.44)
這都是用來判斷那個Model較好的。
p.288 6.5 Poor Data, Collinearity, and Insignificance
homoscedasticity: 同方差性
(看照片)Collieararity
problem:
Nature:
Consequences: var(bk | x) -> infinitry /very big =>
se(bk) go up
如果做hypothesis testing Ho: B2 =0 t=
b2-beta2/se(b2)
(1) Hyporhtsis testomg results will be
unreliable
(2) interval etimates will be incorrect 因為會用到se
會有以上這兩個結果
還有要怎樣 Detection 這個問題?要考慮這個Nature 注意這幾個independent
variable
通常要先看(1)兩個variable的,correlation coefficent
如果很高高到0.7 以上
但如果你有多餘兩個variable的話,要去做correlation coefficent matrix
一對對的去看他的cc值。
這樣檢查只能看出一對一關係,看不出
一群或一對多的collieneariarity關係。
所以還有(2)方法: VIF ‘variance
inflation factor’ 看照片 例5個變數
-
逐一把某個variable拿來當dependent 跑regresion equation,
-
這樣可以看到各個R squate值, (這稱是multiple correlation coefficent
只這個變數對其他所有變數的關係 between x2 to all pther variables
)
教VIF這個好辦法 找出collinearity
- VIF = 1 /(1-R^2) 這樣可以找出每個變數的 VIF (如果R^2增大
VIF就會放大)
- 檢查各個x的VIF 如果R^2>=0.9 (VIF>=10) 有可能是有共線問題 it
might help you to find out, to detect the variable.
(SPE SPSS 都會給VIF 但EViews要自己算)
慢點,還有第(3)招:
如果R^2 很高但 most coefficent are insignificant. 這部可能麻!因為如果R^2很高意思就是所有的x 應該是很fit這個model,所以如果有個x他反而是insignificant那他可能就是問題了。(請看照片 老師寫的公式解釋 var(b2|x) = sigma / (1-…
r 23 指 x2x3的cc 如果寫 r2. (2dot) 指的是x2對其他所有的cc
就是說R^2很高 但t value很小 意思就是這個x2(被當dependent的這個)應是有問題的。
detect
就是用(1)(2)(3)各種方法去找出有問題的variable。
Remedial mesaures: Slove (1) remove 這個verialbe 但未必是最好方法. (2) increase sample size這個方法更好,因為可能久解決問題 (共線可能是sample不足的bias )
那麼什麼時候可以omited這個veriable首先要bae on theory,重要的基本的veriable當然不能remove, 如果次要非必要的就可能可以試試remove. 但加大sample size是重要手段
(3)transform variable (比如把GDP 換成 POP=population) 用另一種變數來取代
,有時不用換,而是換個計算方式比如log這個變數,ln(GDP)。
(4)可能還有其他的罷!但最重要就是以上這三個辦法。
當然還有其他辦法 那要留到下學期教了
看EXAMPLE 6.20 A Logistic Growth Curve
maturarity -> 1
FIGURE 6.2 A Logistic Growth Curve.
公式在(6.52)
讓我們用 steel.wkf 來跑看看
做nonleaning equation:
6.52 打法:
eaf=c(1)/(1+exp(-c(2)-c(3)*t))
當你用EViews作nonleaning equation
時要寫出整個equation 包括等號,不能減省
EXAMPLE 6.19沒有時間講了 Chp6 要到這裡打住了。
Using Indicator Variables
Indicator Variables又稱dummy variables
如果PRICE是房價,SQFT是indepent 而房子與學校的距離,可以做成是個dummy
variable(1表靠近 0表不靠近) 通常用D(當然也可以用別的字)
只有兩個值0,1
Chpter7就是討論這個Indecator variable.
其中有很多問題討論,請自己研究。
有個地方特別重要是: 7.5
Treatment Effects (怎樣用indecator 來做treatment Effects) 這方法稱
DID
Differences-in-Differences 有時也叫DD
去看老師的ppt
接下來兩週都沒有課了,新年快樂,記得交期末報告!明年見。
W17 No class
2025-01-01-Wednesday 14:10-17:00 林師模教授
老師的講義 Ch-08 | 教科書內容 Chapter-08 |
1.當我open with group所有data後,在命令欄執行'smpl if Country = "Japan"'結果所有資料只剩日本這個國家的資料。如果繼續做'smpl if Country = "Canada"'就換成是Canada資料。 如果用[View-Spresheet]應該只看到Japan或Canada資料。
2.[Quick-Estimate Equation]->CSUMPTN C HOURS GOV R INC
due date of final report of QM is 10th Jan. 2025
W18 Final Report
2025-01-08-Wednesday 14:10-17:00 林師模教授
Asig#5-期末的 QM_Final Asig#5_作業草稿 | 老師建議 與Asign#5相關的論文參考html 詳讀 | Asig#5 報告完稿 | 計算用GoogleSheets | AugustineAsig#5作業供參考 |
2025/01/06 Asig#5 交出的作業pdf |
期末作業6.31,操作EViews的過程
2024/01/05與Augustine討論QM_I: Final Report
question:
問題(a)
先要過濾出國家是Japan或Canada,分別用這些dataset做equation estimate
Model是: CSUMPTN = β1 + β2 HOURS + β3 GOV + β4 R + β5INC + e
過濾的方法好多種:
1.直接在command window上下指令 smpl if Country = “Japan” 或
2.用Quick做equation estimate公式是 csumptn c hours gov r inc 執行OK就可。
把這些算出來的stataistic data列出來說明。
問題(b) 是問說如果β2且β3都等於0的話,對cusmptn是如何影響的。
那麼(個別做Japan和Canada) 先用a)model的estimate接著做:
CSUMPTN = β1 + β2 HOURS + β3 GOV + β4 R + β5INC + e
然後選[view]-[coefficient dignostics]-[Wald Coefficent Restrictions]
(Coefficient restrictions
separated b commas)輸入指令如下:
c(2)=0, c(3)=0 (然後按ok執行)
意思是說 當β2 和β3 都是0的話,其他變數的 係數會是怎樣?
這樣就會得到各種test的結果。 可以進行解讀和比較。
問題(c)
本來model是:CSUMPTN C HOURS GOV R INC 現在要把GOV拿掉,model會變成:
CSUMPTN C HOURS R INC (然後用這個去做equation estimate) 跑出資料 可以進行解讀和比較。
問題(d).
此問題提出一個不同的model所以要重作公式如下:
GOV c hours r inc
注意: Japan部份-也可以在Sample欄寫: 1971 2007 if cxid=7
(因為cxid記了各個country的代號,Japan就是7)
問題(e).
那就會到equation a) 的原來的equation estimate
csumptn c hours gov r inc
就是在Sample的地方改為這樣寫 1971 2006 if country=“Japan” (本來是1971 2007)
開始做:Forecast
-跑出equation estimate後-選[forecast]
-在S,E. 打: se 表示要stand error
-然後拿掉勾選□insert actuais for out-of
-sample
-和□forecast graph (目前不要graph)
當跑完資料後,就會產生新的變數hours_forecast。
然後選這個變數hours_forecast用open打開,就會看到數字一路查下去到japan-07 那就是你的forecast 數字
有了這個數字就可算interval,但要注意df是observ數量:36 但失去了5個變數: c hours gov r inc 所以36-5=31。
此外還需要找出se(standard error),方法是:
就是把hurs_forcast和se還有year一起opengroup 然後查到japan-07
就會看到他的se數字了。這可以用來找interval 請看下面:
然後選擇forecast(生出一個新變數)+year+se 去open group。
打開後,往下找到2007年的資料: 這一行
----------------FOREAJPAN-------------SE------------------YEAR
333 Japan - 07 0.008778583943045824 0.01107645865805094 2007
這樣就找到forecast的CSUMPTN值2007年是:0.008779 而SE是: 0.011076
接者要去查表找出t-value
https://www.principlesofeconometrics.com/poe5/poe5tables.pdf
(查TABLE D.2 Percentiles of the t-distribution)找 (0.975,df)
因為df是 36-5=31 從31找到t-value是=2.040
這樣,有了forecast的point(0.008779) 就可用下列公式去算interval:
CSUMPTN2007(0.975,31) +- (t * se-forecast) =
(t-value)2.040 * (se-forecast)0.011076 = 0.2259504 接下去算
Interval是 [(0.008779-0.02259504),(0.008779+0.02259504)]
Interval of CSUMPTN2007(0.975,31)= [-0.01381604, 0.03137404]
再用C model重作一次: point=0.006649
SE=0.011010 接下來要查t表,df只有36個observation(因為只算到2006年)扣除4個變數
(C HOURS R INC 沒有GOV)所以: 36-4 = 32 查t表時要看這個df.所以t-value=2.037
(t-value)2.037 * (se-forecast)0.011010 = 0.02242737 接下去算
Interval是 [(0.006649-0.02242737),(0.006649+0.02242737)]
Interval of CSUMPTN2007(0.975,32)=[-0.01577837 , 0.02907637]
問題f說 model a和c 那一個較好?better fit?
所以比較兩個interval發現model c的比較窄,所以這個比較好!
問題(f):
Backup Data 其他參考資料
Book | D | pdf |
URL | Kaggle | d
R基礎課程02-RStudio介面設定與基本操作
R基礎課程03-R物件資料框 數值 文字 邏輯
R基礎課程04-R函數
R基礎課程05-data table
R基礎課程06、07-正規表達式與迴圈
R基礎課程08-衛生福利資料庫
R基礎課程09-專案演練
中原大學C-learning R language 課程, 2024/10/21報名。
▼1 The Nature of Econometrics and Economic Data
phd16_Chapter_02.ppt
phd16_Chapter_03.ppt
phd16_Chapter_04.ppt
phd16_Chapter_05.ppt
phd16_Chapter_06.ppt
phd16_Chapter_07.ppt
phd16_Chapter_08.ppt
phd16_Chapter_09.ppt
phd16_Chapter_10.ppt
phd16_Chapter_11.ppt
phd16_Chapter_12.ppt
phd16_Chapter_13.ppt
phd16_Chapter_14.ppt
phd16_Chapter_15.ppt
phd16_Chapter_16.ppt
phd16_Chapter_17.ppt
phd16_Chapter_18.ppt
phd16_Chapter_19.ppt
phd16_Regression
phd16_Regression-basics1.2.pptx
phd16_regression
▼2 WHAT IS INFORMATION MANAGEMENT?
WHAT IS INFORMATION MANAGEMENT?
1.ANIMATION FOR PLATONWHAT IS INFORMATION MANAGEMENT? wearesynkro 2014。2. Information Management BasicsCommunity IT Innovators 2018。
3.(IM) Information Management JuanIT 2021。有一系列lecture
4.The 5 Components of an Information System COTC A.R.C. 2015。
▼9 折疊2
折疊2
- Lorem ipsum dolor sit amet.
- Lorem ipsum dolor sit amet.